[데이터분석] 정보 이득(Information Gain) 이해하기(feat. 엔트로피)
정보이득(Information Gain) 개념
정보 이득(Information Gain)은 결정 트리(Decision Tree)에서 엔트로피(Entropy)를 계산 후, 어떤 노드를 선택하는 것이 옳은지 따져볼 때 사용하는 기댓값이다. 결정 트리에서 다양한 노드를 만들고 엔트로피를 구했다면 정보 이득이 가장 높은 값을 선택하고 다음 가지를 생성하게 되기에 엔트로피와 정보 이득은 같이 움직인다 생각하면 된다.

엔트로피
정보 이득에 설명에 사용한 데이터는 이전 엔트로피 계산에 사용한 데이터이며, 엔트로피에 대한 포스팅을 읽고 이 내용을 읽으면 좀 더 이해하기 편할 것 같다.
[데이터분석] 엔트로피(Entropy) 이해하기
보통 엔트로피라 하면 과학 분야에서 많이 쓰이는 말이지만, 통계학 혹은 데이터 분석쪽에서도 곧잘 쓰이는 용어이다. 일단 엔트로피를 가장 많이 활용하는 것 중 하나가 결정 트리(Decision Tree)
needjarvis.tistory.com
이전 데이터는 키와 몸무게를 기반으로 헌병과 그외의 보직을 예측하는 시스템을 결정 트리로 구현하고자 하였다. 이를 기반으로 2가지의 특징을 생성하였는데 하나는 몸무게 75kg 이상이고, 나머지 하나는 키 180cm 이상이었다.
이때 몸무게 75kg 이상은 아래와 같은 엔트로피값이 나왔다.
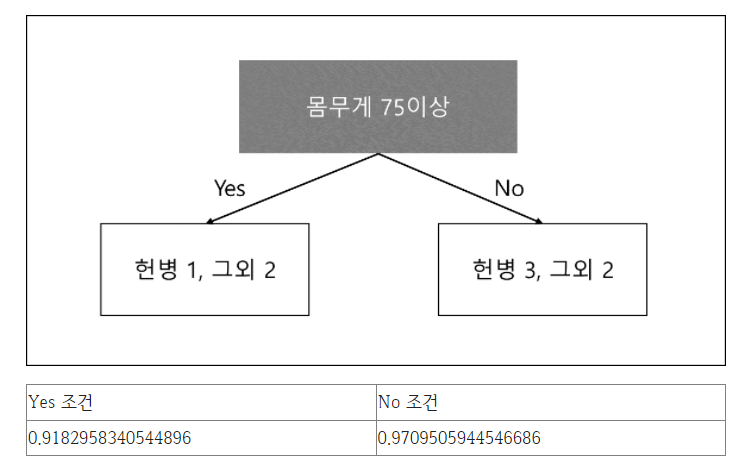
Yes 조건은 약 0.92, No 조건은 약 0.97의 값이 나왔다.
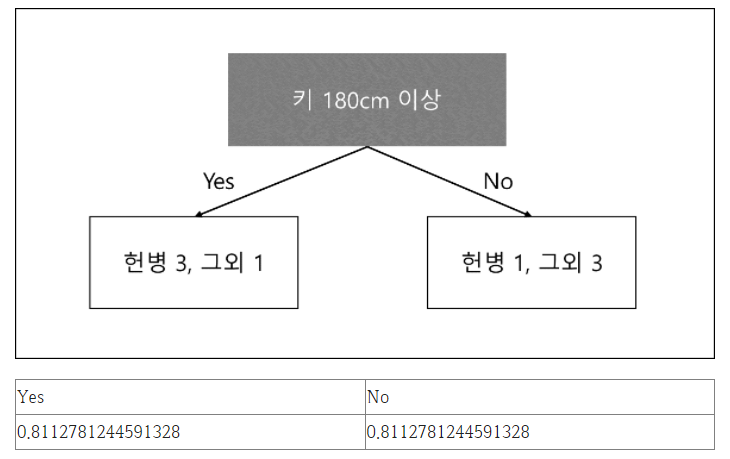
그리고 키 180cm 이상의 조건은
정보 이득 공식
Information Gain = (Entropy before split) - (weighted entropy after split)
정보이득의 공식은 위와 같이 이전 엔트로피의 값을 현재 엔트로피 값들로 뺀 것이다. 이전 엔트로피의 이후의 값들은 이전 엔트로피보다 더 값이 좋아야 되기 때문에 엔트로피 값이 낮을 것이며, 이 둘의 차는 높아질수록 잘 분리된 값이 된다.
이전 엔트로피 값 이후의 엔트로피 값은 2개인데 이것을 어떻게 계산해야 될까? 답은 간단하다. 최종 엔트로피 값에 현재 노드의 비율을 넣으면 된다.
정보 이득 계산
몸무게 75kg 이상 정보 이득
몸무게의 경우 Yes가 3개 였고, No가 2개였기 때문에 값을 3/8과 5/8이라는 값을 추가로 보정해서 계산하게 되면 다음과 같아질 것이다.
소수점 넷째 자리에서 반올림
| 구분 | Yes 조건 | No 조건 |
| 엔트로피 | 0.9183 | 0.9710 |
| 비율 적용 엔트로피 | 0.3444 | 0.6069 |
Weighted Entropy = 0.3444 + 0.6069 = 0.9513
여기에 이전 엔트로피는 1.0이었기에 둘의 값을 빼면
1.0 - 0.9513 = 0.0487
이와 같이 최종 정보 이득 값은 0.0487이 된다.
키 180cm 이상 정보 이득
키의 경우 Yes가 4개, No가 4개였기 때문에 최종적으로 계산된 값을 각각 0.5씩 곱하여 보정한 후 합치면 정보이득 값이 된다.
| 구분 | Yes 조건 | No 조건 |
| 엔트로피 | 0.8113 | 0.8113 |
| 비율 적용 엔트로피 | 0.40565 | 0.40565 |
Weighted Entropy = 0.40565 + 0.40565 = 0.8113
여기에 이전 엔트로피는 1.0이었기에 둘의 값을 빼면
1.0 - 0.8114 = 0.1887
이와 같이 최종 정보 이득 값은 0.1887이 된다.
사실 위의 경우 Yes와 No의 값이 동일하여 계산할 필요가 없었지만 이해를 돕기 위해 그냥 계산을 해보았다.
정보 이득이 높은 노드 선택
최종적으로 키 180cm의 경우 정보 이득이 0.1887이고, 몸무게 75kg 이상인 경우 정보 이득이 0.0487이 되기 때문에 이 경우 키 180cm 이상을 노드에 선택하게 된다.
연관포스팅
결정 트리(Decision Tree) 설명 및 분류기 구현