인공지능 및 데이터과학/자연어처리
문자열 유사도 측정, 편집거리 알고리즘(Levenshtein Distance) 개념 및 Java, Python 예시
Steve Jang
2023. 3. 15. 17:31
편집거리 개념
편집거리 알고리즘(Levenshtein Distance)는 두 개의 문자열 간의 편집거리를 측정하는 알고리즘 입니다. 편집 거리는 문자열을 다른 문자열로 변경하는데 필요한 최소한의 삽입, 삭제 및 대체 작업 수를 나타냅니다.
편집거리 알고리즘은 다양한 응용 분야에서 사용될 수 있는데 맞춤법 검사, 음성 인식, 텍스트 유사성 측정 등에서 사용됩니다.

알고리즘 설명
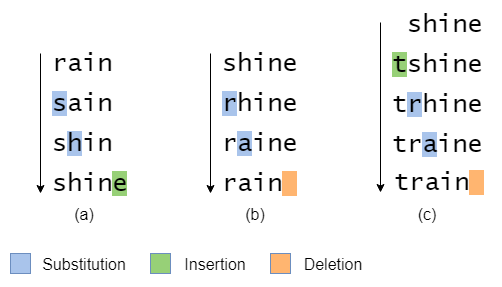
위 예시는 편집거리를 계산하는 것을 보여주는 예시로 비(rain)와 빛나다(shine)로 설명을 합니다. 우선 rain을 shine으로 변환하려면 r을 s로 바꾸고, a를 h로 바꾸고 e를 삽입합니다. 고로 이 편집거리는 3입니다.
기차(rain)와 빛나다(shine)에 대해서 작업을 하게 된다면, shine앞에 t를 붙이고, s를 r로 h를 a로 바꾼 후, 마지막 글자를 삭제하면 train이 되기 때문에 편집거리는 4가 됩니다. 편집거리의 결과를 보면 알겠지만, 거리 값이 짧을수록 두 단어의 유사성이 크다는 것을 의미하게 됩니다.
편집거리 알고리즘 Java 예시
public class MlMain {
public static void main(String[] args) {
String a = "rain";
String b = "shine";
String c = "train";
System.out.println(a + " <-> " + b + " ->" + levenshteinDistance(a, b));
System.out.println(a + " <-> " + c + " ->" + levenshteinDistance(a, c));
System.out.println(b + " <-> " + c + " ->" + levenshteinDistance(b, c));
}
public static int levenshteinDistance(String s1, String s2) {
int m = s1.length();
int n = s2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (int j = 0; j <= n; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = 1 + Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1]));
}
}
}
return dp[m][n];
}
}
예제 결과
rain <-> shine ->3
rain <-> train ->1
shine <-> train ->4
파이썬 예시
def levenshtein_distance(s, t):
m, n = len(s), len(t)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(m+1):
dp[i][0] = i
for j in range(n+1):
dp[0][j] = j
for i in range(1, m+1):
for j in range(1, n+1):
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
return dp[m][n]
print(levenshtein_distance("rain", "shine"))
print(levenshtein_distance("shine", "train"))
//
3
4