딥러닝(Deep Learning)을 이해하기 위해서는 몇가지 개념들을 확실히 익히고 넘어가야 한다. 사실 딥러닝이라는 것은 프로그램적인 요소보다는 이미 만들어진 것을 어떻게 잘 조율해서 사용해야 하는지에 더 달려있기 때문에(요즘 트렌드 자체가 know-where 이기도 하고...) 너무 복잡하게 수식을 이해할 필요도 없고 간단하게 이해하고 넘어가도 딥러닝을 구현하는데 크게 지장이 없을 것이다.
논문을 쓰고 완전히 이쪽길로 깊게 공부하는 사람들은 당연히 수식까지 짜면서 공부를 해야 하겠지만 개발자이기도 하고 딥러닝도 어느정도 핸들링하는 사람들이라면 어느때에 이 기술이 좋더라 정도만 알아도 개발하는데 전혀 지장이 없다.

활성화 함수(Activation Function) 개념
딥러닝은 다양한 레이어(layer)에서 데이터를 연산하고 다음 레이어로 값을 전달해주며 그 레이어에서 또 연산을 하는 식의 구조를 지녔다. 그러다보니 데이터를 연산하면서 정리해야 하는 함수가 필요하게 된다.
예를 들어, 개와 고양이를 분류하기 위해서 우리가 다양한 특징들을 데이터화 시켰다고 가정을 해보도록 한다.
- 털 색깔
- 눈 크기
- 얼굴 크기
- 발 사이즈
기타 등등 수많은 특징(Feature)들로 개와 고양이를 정의하고 이 값들을 학습하여 개와 고양이를 분류하는 것을 만들고자 하는데 데이터를 연산하다보니 튀는 데이터가 있을 수 있고, 필요 없는 데이터가 존재할수도 있을 것이다.
그러면 해당 Feature는 무시해야 하는 상황이 발생할 수 있고, 데이터의 수치가 너무나도 커서 연산을 할 때 모든 연산값이 무너질수도 있을 것이다. 물론 이전에 전처리를 통해서 미리 조절할수도 있지만 수많은 레이어로 이루어진 층에서 연산이 이루어질 때 어떻게 될지는 아무도 알 수 없기 때문에 활성화 함수라는 함수를 만들어서 데이터의 폭을 어느정도 정의할 수 있는 것이다.
계단(Step) 함수
최초의 신경망이 퍼셉트론인 것처럼 퍼셉트론에서 최초로 사용한 활성화 함수가 바로 계단 함수이다.

그래프의 모양처럼 0이라는 값을 기준으로 값이 0에서 1로 극심한 차를 보인다. 한마디로 0혹은 1로만 이루어진 것이 계단함수이며 0이상이면 1, 0 미만이면 0인 활성화 함수이다.
python으로 구현한 계단함수의 개념
def step ( val ):
if(val >= 0):
return 1
return 0
계단함수는 데이터가 극적으로 변하는 모양새이기 때문에 데이터의 손실이 일어날 가능성이 있기 때문에 딥러닝에서는 사용되지 않는 활성화함수이다. 매우 간단한 분류같은 것은 계단함수로도 어느정도 가능하겠지만, 딥러닝이 필요한 데이터는 매우 다양한 데이터가 있기 때문에 계단함수로 구현할 경우 낮은 성능을 보여주게 될 것이다.
시그모이드(Sigmoid) 함수
시그모이드(sigmoid) 함수는 딥러닝 혹은 신경망을 배우는 사람이라면 step activation function을 배우자마자 바로 다음에 배우는 기초 함수중 하나이다.
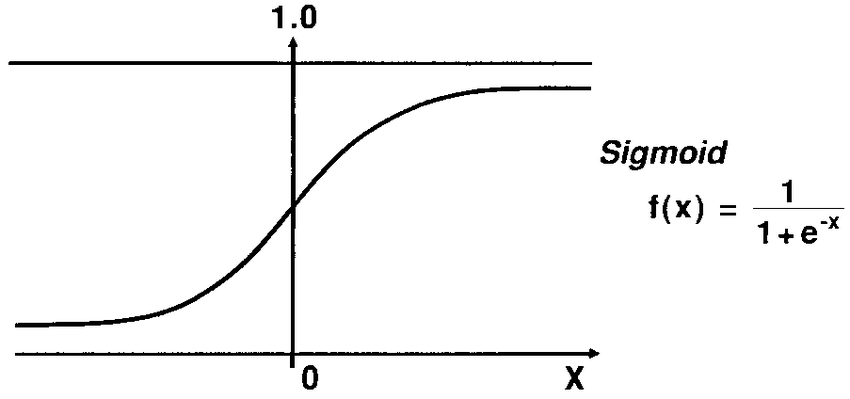
시그모이드 함수는 계단함수의 단점인 미세한 값을 생성할 수 있게 나온 함수이다. 계단함수가 0과 1로만 된 함수라면 시그모이드는 0과 1사이의 실수로 이루어진 함수이기 때문에 0.237 등과 같이 정교한 수를 전달할 수 있다.
계단함수는 "아마도"라는 것이 불가능하다. 0과 1로만 되어 있기 때문에 "이건 이거야 이건 아니야"라는 느낌의 함수라면 시그모이드는 "이건 아마 이정도의 값이야"를 표현해주게 되는 것이다.
그러나 시그모이드 역시 단점이 존재하는데 대표적으로 vanishing gradient이라는 문제를 발생시키는 것이다. 입력값이 아무리 커도 미분 값의 범위가 제한됨으로써 층이 많을수록 gradient 값이 0에 수렴하는 문제를 가지고 있다.

이해가 안될 수 있는 분들을 위해서 간단히 설명을 하자면, 시그모이드는 값을 0과 1사이로 변환해주는 역할을 해주기 때문에 아무리 값이 많아도 데이터를 0과 1사이로 변환시켜버린다. 한마디로 엄청나게 큰 데이터를 조그마한 데이터로 꾸겨넣기 때문에 발생하는 side-effect 정도로 이해하면 될 것 같다.
딥러닝은 기울기라는 것을 이용해서 값을 찾아나아가는데 층이 많아지면 점점 값이 0에 수렴되어버리는 문제가 발생하여 성능이 떨어지게 된다. 이런 문제를 기울기가 사라지는 문제(vanishing gradient problem)이라고 하며 추후 설명할 ReLU 활성화 함수는 이런 문제를 극복하기 위해서 나오게 된다.
하이퍼볼릭탄젠트(Tanh) 함수
Tanh가 기울기 문제를 해결하면 좋겠지만, sigmoid가 0과 1사이의 실수를 계산해주는 것 대신 -1과 1사이의 값으로 계산해주는 녀석이다.
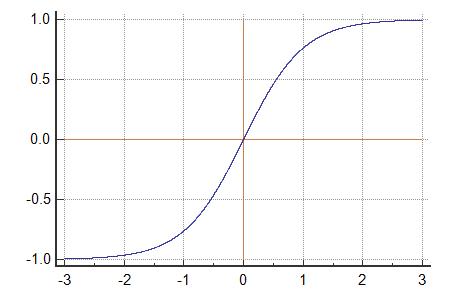
그러다보니 시그모이드의 단점을 몇가지 해결하였는데 값의 중심이 0이라는 것이다. 시그모이드는 값의 중심이 0이 아니기 때문에 여러가지 문제점이 발생할 수 있었다.
다만 그래프의 모양을 보면 알겠지만, 시그모이드와 함수와 유사하게 기울기가 사라지는 문제는 이놈 역시 고질적으로 가지고 있는 함수이다.
ReLU(Rectified Linear Unit) 함수
현재 가장 많이 사용하는 활성화 함수를 뽑자면 ReLU함수를 뽑을 수 있을 것 같다.
이 함수는 f(x) = max(0, x) 라는 매우 간단한 수식으로 0이하는 0으로 고정하고 0 값을 초과할 경우 해당 값을 그대로 출력하는 매우 심플한 구조이다.

ReLU는 데이터를 0과 1사이로 꾸겨넣지 않기 때문에 sigmoid와 tanh에서 발생하는 vanishing gradient problem이 발생하지 않는다. 그래서 레이어가 많아져도 원활한 학습이 가능하며 성능(학습속도)도 매우 뛰어나기 때문에 인기가 많다.
ReLU에서 쓰이는 연산은 단 세 개의 명령으로 충분하지만, 시그모이드의 경우 수 십배나 명령이 많기 때문에 둘간의 연산의 차이가 날 수 밖에 없다.
ELU 함수
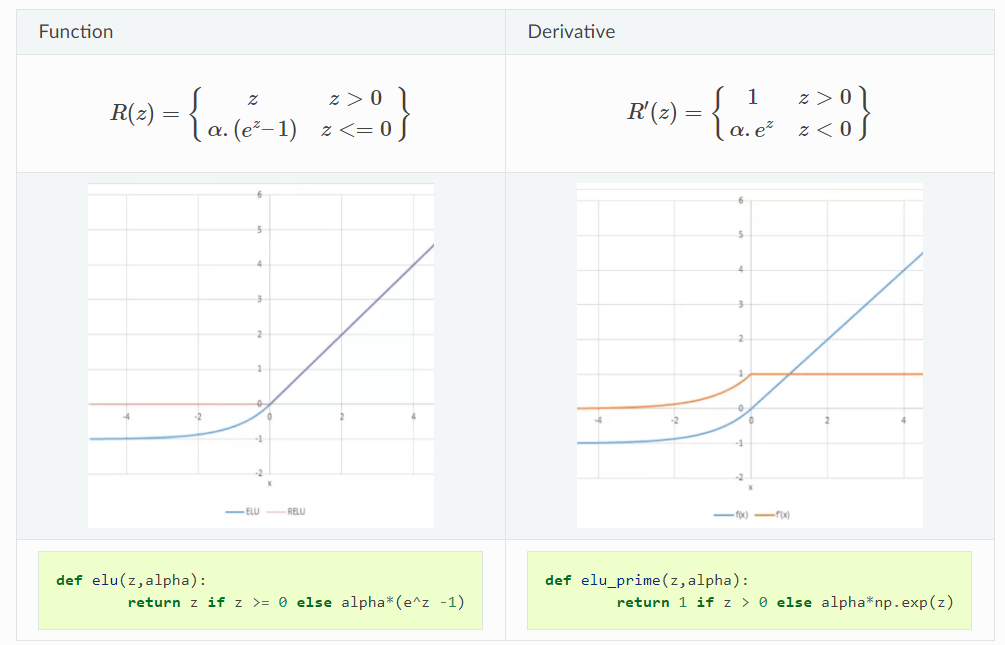
ReLU은 값이 0이하일 땐 모두 0으로 변경을 하기 때문에 Dying ReLU(뉴런이 0을 출력하여 더이상 학습이 안되는 문제)와 같은 문제가 발생할 수 있다. 이를 막고자 나온 개념 중 하나가 ELU function이다.
LeakyReLU 함수
ELU와 마찬가지로 LeakyReLU 역시 Dying ReLU를 방지하는 함수이다.

ELU와 leakyReLU의 차이점은 0이상일 땐 ReLU와 동일한 모습을 보여주지만, 0미만일땐 leaky는 선형적이고 ELU는 비선형적인 모습을 가지고 있다.
leakyReLU는 ReLU의 dying ReLU를 해결하기 위해서 나온 대안책으로 ReLU보다 무조건 성능이 좋다는 것은 아니다. 모든 펑션들은 장단점들이 있으며 프로젝트 상황에 따라 적절한 함수를 써봐야 된다. 그렇기에 딥러닝은 엔지니어적인 관점도 큰 분야이다.
Softmax 함수
Softmax는 활성화 함수이지만 그래프가 존재하지 않는 함수이다. softmax를 사용하는 경우 결과를 확률로 변경하게 된다. 즉 마지막의 결과가 분류를 해야 되는 것이라면 softmax를 써서 모든 결과가 1로 수렴하게 만들 수 있다.
참고자료
https://ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html
'인공지능 및 데이터과학 > 머신러닝 및 딥러닝' 카테고리의 다른 글
| [딥러닝] 척도(Metrics)의 설명 및 종류 (1) | 2020.08.03 |
|---|---|
| [딥러닝] 목적/손실 함수(Loss Function) 이해 및 종류 (0) | 2020.08.03 |
| 추천시스템(Recommender System) (0) | 2020.01.03 |
| 경사 하강법(Gradient Descent) 최적화 알고리즘 (0) | 2018.11.20 |
| 챗봇 및 기계번역에 특화된 문장 학습 모델, 시퀀스 투 시퀀스(Seq2Seq) (0) | 2018.03.30 |