정규화의 기반이론인 함수적 종속성(Functional Dependency)
- 정보처리기술사/데이터베이스
- 2020. 11. 28.
함수적 종속성(Functional Dependency)의 개요
함수적 종속성의 개념
- 데이터베이스(Database, DB)의 릴레이션(Relation)에서 두 개의 애트리뷰트(attribute) 집합 간 제약의 일종
- 데이터들이 어떤 기준값에 의해서 항상 종속이 되는 현상
- Y는 X에 함수적으로 종속된다라고 정의하고 X -> Y로 표기
- X를 결정자(determinant set)라 하고, Y는 종속자(dependent attribute)라 한다.
함수적 종속성의 필요
- 종속된 테이블에 데이터를 배치하여 반복 차단
- 이상현상을 제거할 경우 데이터의 정합성을 유지할 수 있음
- 정규화 작업 수행 시 가장 중요한 작업으로 제2 정규형에서 BCNF까지 적용
함수 종속 다이어그램 (Functional Dependency Diagram, FDD)

기능 종속성 다이어그램 (FDD)에서 기능 종속성은 속성을 나타내는 사각형과 종속성을 나타내는 무거운 화살표로 표시됩니다. 그림은 가장 단순한 기능적 종속성 즉, FD : Y-> X에 대한 기능적 종속성 다이어그램을 보여줍니다. 기능적 종속성 다이어그램에서 각 FD는 수평선으로 표시됩니다 . FD의 왼쪽 속성, 즉 결정자 는 FD를 나타내는 선 에 수직선 으로 연결됩니다 . 오른쪽 속성은 속성을 가리키는 화살표로 연결됩니다.
example)
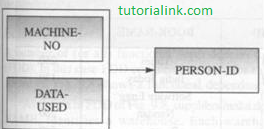
FD : {MACHINE-NO, DATA-USED}-> {PERSON-ID}
위 그림은 한 사람이 기계에서 작업하는 것을 기능적 종속성으로 표현한 다이아그램
함수 종속의 유형
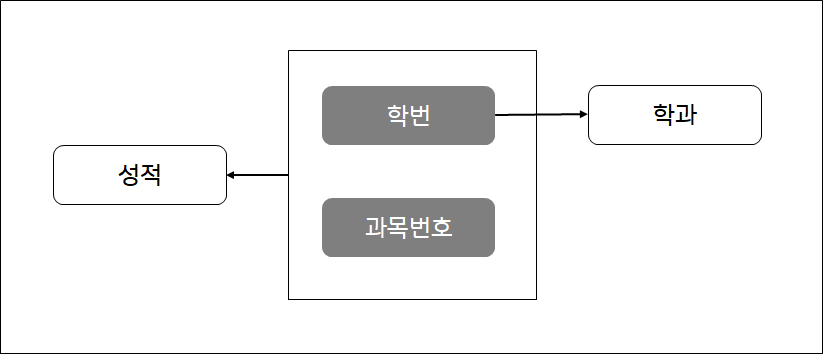
완전함수 종속성(fully functional dependency)
- X’⊂X 이고 X’→Y 를 만족하는 애트리뷰트 X'이 존재하지않음
- {학번, 과목번호} → 성적
부분함수 종속성(partial functional dependency, 2NF)
- X’⊂X 이고 X’→Y 를 만족하는 애트리뷰트 X'이 존재함
- 학번 → 학과
- 완전 함수적 종속성은 이미 정규화가 되어 있기에 정규화 대상이 아님
- 부분 함수적 종속성은 2차 정규화 대상

이행함수 종속성(transitive dependence, 3NF)
- 릴레이션 R에서 속성 A→X이고 X→Y이면 A→Y
- 학번 → 지도교수, 지도 → 교수학과, 학번 → 학과
- 3차 정규화 대상
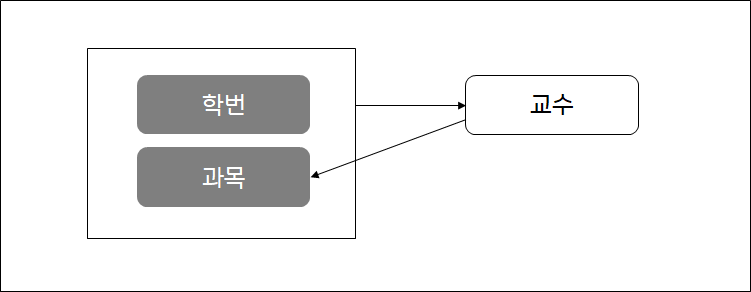
결정자함수적 종속성(boyce-codd normalization, BCNF)
- 함수적 종속성이 되는 결정자가 후보키가 아닌 경우 (X→Y에서 X가 후보키가 아님)
- 교수 → 과목
- Boyce/Codd 정규화 대상
다중값 종속성(Multi-Valued Dependency, MVD, 4NF)
- 한 관계에서 둘 이상의 독립적인 다중값 속성이 존재하는 경우
- X, Y, Z 세개의 속성을 가진 릴레이션 R에서 속성쌍[X,Z]값에 대응하는 Y값의 집합이 X값에만 종속되고 Z값에는 독립이면 Y는 X에 다중값 종속된다고 하고 X->>Y로 표기
조인종속성(Adjoin Dependency, 5NF)
- 관계 중에서 둘로 나눌 때는 원래의 관계로 회복할 수 없으나, 셋 또는 그 이상으로 분리시킬 때 원래의 관계를 복원할 수 있는 특수한 경우
함수 종속의 추론규칙(Armstrong's axioms, 암스트롱의 공리)
기본
반사의 공리(Reflective)
- Y가 X의 부분 집합이면, X → Y이다.
확대의 공리(Augmentation)
- X → Y이면, XZ → YZ이다.
이행의 공리(Transitivity)
- X → Y이고 Y → Z이면 X → Z이다.
위 기본 추론 규칙들로 인해 부수적인 법칙을 유도해 낼 수 있음
부가
합집합의 성질(Union)
- X → Y이고 X → Z이면 X → YZ이다.
분해의 성질(Decomposition)
- X → YZ이면 X → Y이고 X → Z이다.
유사 이행적 성질(Pseudo-Transivity)
- X → Y이고 YZ → W이면, XZ → W이다.
키워드
결정자/종속자, 완전 함수종속성, 부분 함수종속성, 이행 함수종속성, 결정자 함수종속성, 다중값 함수종속성, 조인종속성, 암스트롱 공리, 반사의 공리, 확대의 공리, 이행의 공리, 합집합의 성질, 분해의 성질, 유사 이행적 성질
참고자료
https://ko.wikipedia.org/wiki/%ED%95%A8%EC%88%98_%EC%A2%85%EC%86%8D
https://tutorialink.com/dbms/functional-dependency-diagram%C2%A0and-examples.dbms
'정보처리기술사 > 데이터베이스' 카테고리의 다른 글
| 엔터티(Entity)를 구분하는 식별자(Identifier) (0) | 2021.01.31 |
|---|---|
| 데이터베이스의 논리적 작업단위, 트랜잭션(Transaction) (0) | 2020.11.28 |
| 데이터베이스의 연결함정(Connection Trap) (0) | 2020.11.27 |
| DB 무결성 확보를 위한, 동시성 제어(Concurrency control) (0) | 2020.10.07 |
| DB의 분산처리 기법, 샤드(Shard), 샤딩(Sharding) (0) | 2020.08.14 |