확률적 경사하강법은 대표적이고 인간에게 아담과 같은 존재인 경사 하강법(Gradient Descent, GD)에게서 파생된 최적화 알고리즘(Optimizer, 옵티마이저)이다.
일단 본 포스팅에 앞서 경사 하강법에는 Mini Batch Gradient Descent도 있지만 보통 mini batch를 SGD를 포함시켜서 mini batch의 특징도 SGD로 설명 하였다.

경사 하강법의 단점과 확률적 경사하강법의 원리
그러나 GD에게는 치명적인 단점이 있는데 바로 한스텝 내딛을 때마다 전체 데이터를 이용하는 단점이 있다. 이를 등산으로 비교하자면, 내가 한걸음 옮길 때마다 지도랑 나침반보고 갈길 정한다는 것과 같다. 대충 들어도 엄청 비효율적인것 같지만 반면에 성능자체는 꽤 괜찮게 나올 수 있다는 것도 대충 들어 알 수 있다.
GD는 바로 이러한 비효율적인 방식을 개선한 트레이드 오프 알고리즘이다.

이 그림만 보면 Stochastic 방식을 왜 쓰는가? 생각할 수 있다. GD의 경우 올바른 방향으로 쭈욱 가는 반면 SGD는 이상한 방향으로 가다가 결국에 목표에 도착하기 때문이다. 하지만 이 그림만보고 GD가 좋다 판단할 수 없는 것이 결국 목표지점까지 제대로 도착 했다면 얼마나 걸렸는지가 핵심이기 때문이다.
미니 배치(Mini batch) 이용
GD가 한발자국 갈때마다 지도 열고, 나침반 키는 대신에, SGD는 일단 방향 잡고 쭈욱 걷고 일정 시간이 지나면 다시 나침반 켜고, 지도 펼쳐서 다시 쭈욱 가는 방식이기 때문에 결론적으로는 누가 위라고 장담하기 힘들다 이는 데이터의 셋이 얼만큼 있는지 상황이 어떤지에 따라 성능이 갈리기 때문이다.
GD가 전체 데치터셋으로 매걸음 방향(매개변수 갱신)을 산정하는 대신 SGD는 Mini Batch를 이용해서 데이터를 조금씩 훑고 쓰윽 지나가며 업데이트한다.
SGD의 단점
이와 같이 매우 단순하고 구현이 편리하지만 상황에 따라 매우 효율이 떨어지는 경우가 많은데 비등방성(anisotropy) 함수와 같이 방향에 따라 기울기가 달라지는 함수에 대해서는 매우 비효율적이다.
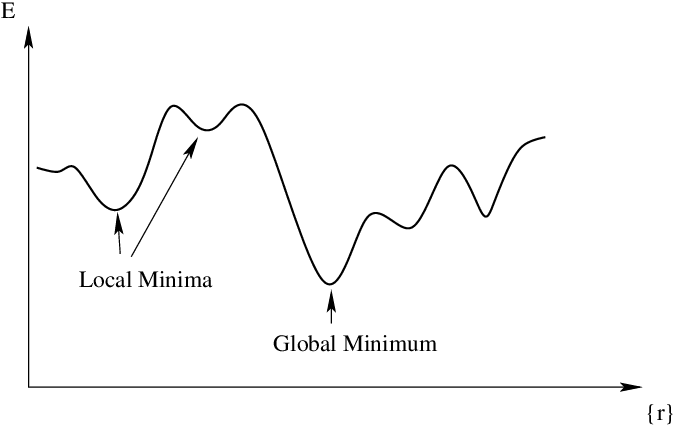
게다가 학습률(Learning rate)가 낮으면 곧장 최적화하지 못하고 지그재그로 이동하게 되면서 지역 최소값(local minimum)에 갇혀 빠져나오지 못하는 경우가 있고, 학습률이 높으면 최적화 자체를 실패할 수 있는 문제가 있다.
'인공지능 및 데이터과학 > 머신러닝 및 딥러닝' 카테고리의 다른 글
| 전이 학습(Transfer Learning) (1) | 2021.12.06 |
|---|---|
| [머신러닝] 모멘텀(Momentum), NAG 옵티마이저 (0) | 2021.06.19 |
| [머신러닝] 옵티마이저(Optimizer)란? (0) | 2021.06.05 |
| [딥러닝] 순환신경망(RNN)과 LSTM, GRU (0) | 2021.06.01 |
| 머신러닝의 작업 플로우(Workflow) (0) | 2021.05.24 |