K-means 자체에 대해서 아직 이해가 부족하신 분은 예전 포스팅에 자세히 적은 것이 있기 때문에 이전 포스팅을 먼저 보면 될 것 같으며 아래 링크를 확인하면 된다.
클러스터링(Clustering)을 통한 데이터 분류기법, K-평균(K-Means) 알고리즘
K-평균(K-Means) 알고리즘은 기계학습(머신러닝, machine learning), 데이터마이닝에서 활용하고 있는 기법으로서, 대표적인 비지도학습이다. 비지도학습이란 어떤 결과를 예측하지 못해야 되는 것으
needjarvis.tistory.com
K-means를 알고 계신 분들에게 다시 한번 간단히 상기시키면 다음과 같은 순서로 클러스터링이 작동된다.
- 중심점인 K를 지정한 후, 이 값은 무작위의 좌표값으로 시작된다.
- 데이터 요소들과 무작위의 중심점(centroid)간의 거리를 계산한다. 다른 거리 측정 알고리즘을 사용해도 상관 없지만 일반적으로는 유클리드 거리를 사용하며 계산한다.
- 데이터 요소들을 가장 가까운 중심점에 속하게 만든다.
- 중심점은 자신들이 속한 데이터 요소들의 중심으로 이동한다.
- 2~4의 작업을 반복하며, 더이상 K 중심점들이 이동하지 않을 경우 알고리즘을 종료한다.
K-means는 이렇듯 쉬우면서도 강력한 클러스터링 효과를 보여주기 때문에 비지도학습인 클러스터링 알고리즘 중 상징적인 알고리즘으로 자리잡고 있다.
그럼 이제 sklearn 라이브러리에서 제공하는 kmeans 클러스터링을 실습해보도록 한다.
K-means 클러스터링 예제
라이브러리
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
샘플 생성
sklearn에서 제공하는 make_blobs으로 샘플을 생성하고, 이 값을 matplotlib의 pyplot에 담는다.
# 랜덤값 고정
np.random.seed(8)
X, y = make_blobs(n_samples=1000, centers=4, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], marker='.')위 내용의 값을 확인하고 싶으면, plt.show()를 넣어보면 되며, pyplot을 중간에 실행하면 다음과 같은 차트가 보여진다. np.random.seed로 값을 부여한 것은 실습때 동일한 결과를 얻기 위함이며, 랜덤 시드 부분은 삭제해도 무방하다.
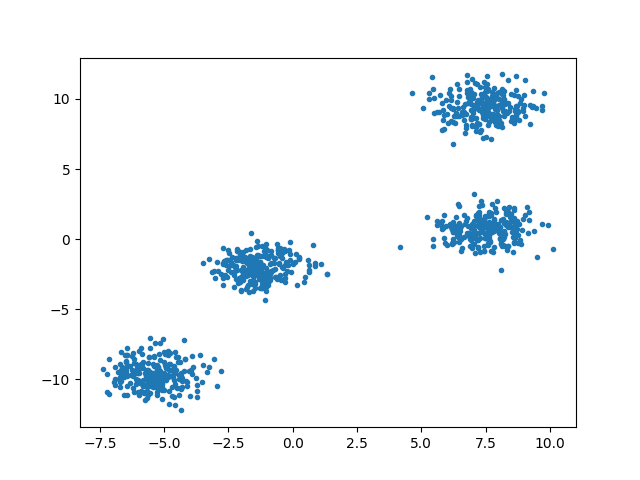
학습 진행
KMeans을 생성한다. K는 n_clusters이며, 여기서는 4개를 세팅하였다. n_init은 다른 중심 시드로 실행되는 횟수로 12회로 세팅되었다. 추가적인 파라미터가 궁금하면 최하단의 [1] 링크를 확인하면 된다.
k_means = KMeans(init="k-means++", n_clusters=4, n_init=12)
k_means.fit(X)
학습 결과 확인
fit이 완료되었으면, labels_라는 레이블 결과와 cluster_centers_라는 중심점 값이 만들어진다.
k_means_labels = k_means.labels_
print('k_means_labels : ', k_means_labels)
k_means_cluster_centers = k_means.cluster_centers_
print('k_means_cluster_centers : ', k_means_cluster_centers)
위 코드의 print 결과
k_means_labels : [0 1 3 2 0 0 3 2 3 2 2 0 0 3 1 3 1 1 0 1 0 0 0 2 3 3 2 0 2 1 3 1 0 1 0 0 0
0 2 2 2 0 0 3 0 2 3 2 3 1 1 3 0 0 2 1 3 2 3 2 3 3 3 3 3 1 2 1 1 1 1 0 1 2
3 3 3 3 1 3 0 0 3 2 1 3 3 1 2 0 0 1 0 1 1 2 3 2 0 3 2 3 1 1 0 2 1 1 2 1 2
2 1 0 1 3 0 3 3 1 3 2 0 2 3 3 0 2 0 1 1 0 3 2 3 1 3 1 2 0 0 0 2 2 3 3 0 0
3 1 1 3 3 2 2 3 0 2 2 1 2 3 0 0 3 3 1 0 1 2 3 3 0 2 0 2 0 1 3 1 3 2 0 3 3
3 0 3 1 2 1 3 2 0 3 2 3 2 3 1 1 2 3 1 1 1 3 3 2 2 3 2 2 1 0 2 0 1 1 2 1 1
0 1 3 2 0 1 0 2 2 2 3 3 0 3 0 2 1 0 3 1 2 2 0 3 3 2 2 1 1 3 1 3 2 2 0 2 3
1 1 3 1 2 3 3 3 3 0 2 0 0 1 3 3 2 1 1 2 3 2 2 1 3 2 2 2 1 2 1 0 2 1 0 3 0
2 1 0 1 1 3 0 2 3 0 2 3 3 2 0 2 3 0 1 2 3 1 3 0 0 3 3 0 0 0 3 1 0 0 2 0 1
1 3 1 3 2 1 2 3 3 0 3 0 0 3 0 2 3 2 1 1 2 3 0 3 1 2 0 0 1 1 3 2 3 3 3 0 3
1 3 0 1 0 1 2 0 3 3 1 1 0 1 2 2 1 0 2 1 1 3 0 0 2 2 3 3 1 3 2 1 0 0 3 3 1
3 2 2 3 0 1 2 0 1 2 3 0 0 1 1 0 1 0 1 2 2 0 0 3 0 2 0 0 2 0 3 3 1 1 3 3 1
2 0 1 2 0 0 1 2 3 1 2 3 2 1 2 1 0 0 1 3 2 0 0 1 1 1 0 2 0 1 1 2 0 3 3 0 3
0 2 1 3 3 3 3 3 2 1 2 3 0 2 2 1 2 0 1 2 3 2 0 3 2 2 3 3 3 1 2 2 2 0 1 2 0
1 0 0 0 3 2 1 1 2 0 3 1 1 0 1 0 0 3 0 2 0 0 0 0 2 3 1 2 2 0 3 1 1 2 3 0 3
0 3 3 0 2 3 0 1 3 0 0 2 1 1 2 3 0 0 0 3 0 0 0 1 1 1 2 1 1 2 2 2 2 2 1 1 2
2 0 3 1 3 0 3 2 2 3 2 1 1 2 3 0 0 3 2 0 0 1 3 2 1 2 2 2 1 0 2 1 0 0 2 1 1
3 2 1 1 2 1 3 1 0 3 0 1 1 3 0 1 1 2 3 1 2 2 3 0 1 1 2 3 0 3 0 2 1 3 2 0 1
0 0 1 2 3 1 2 3 2 3 3 2 1 1 1 2 1 0 0 0 3 1 2 1 0 0 0 0 3 2 0 1 2 0 0 0 0
0 1 0 3 0 3 0 1 2 0 1 2 1 0 0 1 2 1 2 0 1 3 0 0 2 0 3 3 0 1 1 0 3 0 2 2 2
0 2 1 3 3 2 1 3 3 1 3 1 3 1 0 1 0 3 1 1 3 3 2 2 2 3 3 2 3 1 1 0 1 0 2 2 0
0 0 1 3 0 3 0 1 3 2 3 3 2 0 2 0 3 1 1 1 1 0 0 0 2 1 0 2 3 1 3 2 1 2 2 0 2
3 2 2 3 2 3 1 3 3 2 2 2 3 2 3 2 2 1 3 3 2 2 3 2 3 0 2 2 0 1 1 1 3 1 3 2 3
0 1 1 0 0 0 2 1 3 0 2 1 2 3 1 2 2 1 2 1 1 0 0 2 3 3 2 2 1 3 3 0 1 3 1 3 1
2 0 2 0 3 3 1 0 2 0 2 0 0 3 1 2 1 2 1 3 3 3 2 3 0 0 1 3 1 0 0 2 1 2 3 2 1
2 1 0 0 2 1 2 0 1 1 2 0 1 3 0 3 0 1 2 0 0 0 2 3 1 3 1 0 3 3 2 2 2 3 2 3 0
0 3 0 2 0 0 3 1 1 0 3 2 0 0 3 1 2 1 1 1 1 3 2 1 0 2 1 2 3 3 1 3 0 1 1 2 1
2]
k_means_cluster_centers : [[ 7.43677253 0.6966818 ]
[ 7.44207714 9.40391707]
[-5.35905231 -9.6306923 ]
[-1.32469127 -1.9919531 ]]
값을 만들어 냈으면, 이제 시각적으로 확인해 보도록 한다.
K-means Clustering 시각화
# 지정된 크기로 초기화
fig = plt.figure(figsize=(6, 4))
# 레이블 수에 따라 색상 배열 생성, 고유한 색상을 얻기 위해 set(k_means_labels) 설정
colors = plt.cm.Spectral(np.linspace(0, 1, len(set(k_means_labels))))
# plot 생성
ax = fig.add_subplot(1, 1, 1)
for k, col in zip(range(4), colors):
my_members = (k_means_labels == k)
# 중심 정의
cluster_center = k_means_cluster_centers[k]
# 중심 그리기
ax.plot(X[my_members, 0], X[my_members, 1], 'w', markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col, markeredgecolor='k', markersize=6)
ax.set_title('K-Means')
ax.set_xticks(())
ax.set_yticks(())
plt.show()
최종결과

위 내용을 실행하면, make_blob으로 만들어진 pyplot과 레이블로 색깔이 칠해진, 결과 2개의 pyplot이 띄워질 것이며 위 내용은 2번째 레이블이 된 pyplot 결과이다. 이처럼, K-means가 잘 작동 된 것을 확인할 수 있다.
최종 소스
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 랜덤값 고정
np.random.seed(8)
X, y = make_blobs(n_samples=1000, centers=4, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], marker='.')
k_means = KMeans(init="k-means++", n_clusters=4, n_init=12)
k_means.fit(X)
k_means_labels = k_means.labels_
print('k_means_labels : ', k_means_labels)
k_means_cluster_centers = k_means.cluster_centers_
print('k_means_cluster_centers : ', k_means_cluster_centers)
# 지정된 크기로 초기화
fig = plt.figure(figsize=(6, 4))
# 레이블 수에 따라 색상 배열 생성, 고유한 색상을 얻기 위해 set(k_means_labels) 설정
colors = plt.cm.Spectral(np.linspace(0, 1, len(set(k_means_labels))))
# plot 생성
ax = fig.add_subplot(1, 1, 1)
for k, col in zip(range(4), colors):
my_members = (k_means_labels == k)
# 중심 정의
cluster_center = k_means_cluster_centers[k]
# 중심 그리기
ax.plot(X[my_members, 0], X[my_members, 1], 'w', markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col, markeredgecolor='k', markersize=6)
ax.set_title('K-Means')
ax.set_xticks(())
ax.set_yticks(())
plt.show()
References
[1] scikit-learn.org -KMeans, https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
[2] coursera - Machine Learning with Python
연관포스팅
클러스터링(Clustering)을 통한 데이터 분류기법, K-평균(K-Means) 알고리즘
'인공지능 및 데이터과학 > 머신러닝 및 딥러닝' 카테고리의 다른 글
| [Python] DBSCAN 클러스터(Clustering) 구현하기 (0) | 2022.02.13 |
|---|---|
| DBSCAN clustering 이해하기(밀도기반 알고리즘) (0) | 2022.02.12 |
| KNN(k최근접) 알고리즘 설명 및 구현하기 (0) | 2022.01.31 |
| 결정 트리(Decision Tree) 설명 및 분류기 구현 (0) | 2022.01.17 |
| [Python] 해밍 거리(Hamming distance) 이해 및 구현하기 (0) | 2022.01.13 |